t検定
概要
本ページ内では、t検定を終着点とした一連の分析の手順についてまとめます。t検定は、2つのグループ間の平均値に有意な差があるかを分析する手法です。ただ、その分析をするためには、通常以下のような流れを踏む必要があります。
まず、本コンテンツでは分析にHADを用いますので、それをダウンロードして使える状態にする必要があります(1:分析ソフトとデータの準備)。次に、心理学の研究では、多くの場合、複数の項目を使って1つの概念を測定することが行われます。そうした場合に、複数の項目を本当に1つの変数として扱っていいのかをチェックする必要があります(2:変数の合成)。さらに、t検定の前に、それぞれの変数の平均値や標準偏差、相関係数をチェックし、それぞれの変数の特徴を記述します(3:記述統計)。ここまでが完了してようやく一番したい分析を実行することができます(4:t検定の実行)。分析が終わったら、心理学論文の書き方に沿って、表をまとめ(5:表の作成)、文章で記述してください(6:論文の記述)。
1.分析ソフトとデータの準備
まず分析に用いるHADを使える状態にしてください。これがまだできていない方はこちらのページから準備をしてください。
次に、分析に用いるデータを準備し、HADに入力してください。Qualtricsで収集したデータを使われる方はこちらのページでやり方を確認してください。
ここでは刑事司法に対する態度(これについてはこちらのページをご参照ください)、犯罪不安、性別を含んだデータを分析に用います。研究の目的としては、犯罪者に対して厳しい刑罰を求める態度や犯罪不安には性差があるのかを検討する想定です。このデータはこちらからダウンロードできます。ご自身のデータがある方はそれを使ってください。
2.変数の合成
多くの心理学的な研究では、1つの構成概念を測定するために複数の項目を用意するといったことが行われます。今回のデータでも、刑事司法に対する態度と犯罪不安はそれぞれ複数の項目で測定されています。
ただ、複数の項目が1つの構成概念をきちんと測定できているかは確認する必要があります。そのために用いられる統計的な手法は、①因子分析と、②信頼性係数(α係数)の確認です。どちらを使うかは先行研究で因子構造が確認されているかどうかによります。より端的には、自分で作成した尺度(項目)である場合や先行研究の尺度を変更した場合には因子分析を行う必要があります。これに対して、先行研究で用いられている尺度をそのまま使っている場合には因子分析をする必要はなく、信頼性係数を求めれば十分です。ご自身の計画がどちらに当てはまるかを確認してください。
なお、分析・判断は変数ごとに行う必要があります。たとえば、変数Aは先行研究のものをそのまま使っているが、変数Bは自分で新たに作成したものである場合には、変数Aは信頼性係数を求めるだけで足りますが、変数Bについては因子分析を行う必要があります。変数ごとに個別に判断してください。
ここで使われている変数(刑事司法に対する態度と犯罪不安)は実際には先行研究で因子構造が確認されています(つまり、何個の因子に分かれるかはすでに示されています)。ですので、本来であれば因子分析をする必要はありませんが、あくまで例として因子分析も行っています。自分のデータを使って分析する方はご注意ください。
因子分析
まずデータを確認します。今回のデータでは、厳罰傾向を測定する項目は3個あり、cj_1からcj_3までの列に入力されています。因子分析ではこれらのデータを使いますので、これらをコピーして、「id」の横に貼り付けてください。
移動ができたら、「因子分析」にチェックを入れてください。
因子分析の前に、因子数を決める必要があります。「スクリープロット」を左クリックしてください。
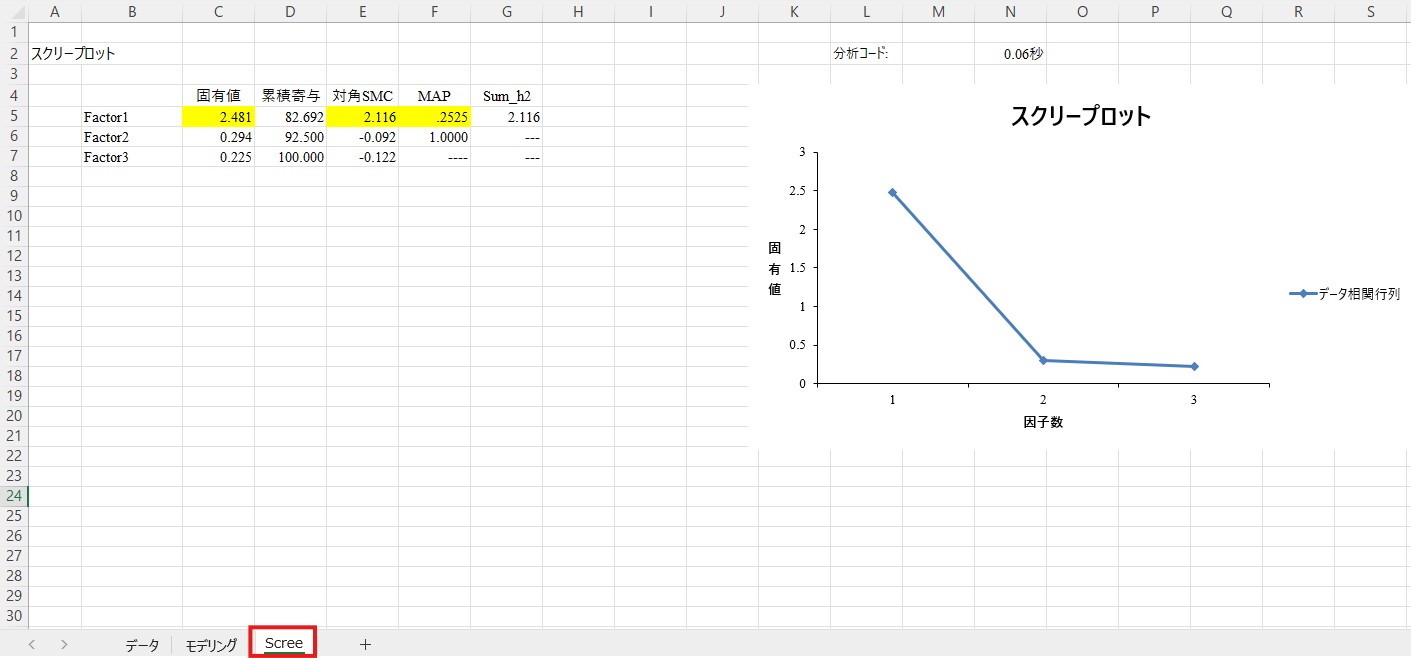
「Scree」というシートが新たに作成されれば成功です。
このシートには、固有値や累積寄与、対角SMCの値などが表示されています。これらの数値から因子数を決定する手法には色々なものがありますが、初学者の方にとっては固有値で色が付いている因子数を選択するのが最も楽かと思います。ここでは「Factor1」に色が付いていますので、1因子構造が妥当であると判断できます。
もう一度「モデリング」のシートに戻り、「因子数」に「1」を入力してください(必ず半角で入力してください)。
「分析実行」を左クリックしてください。
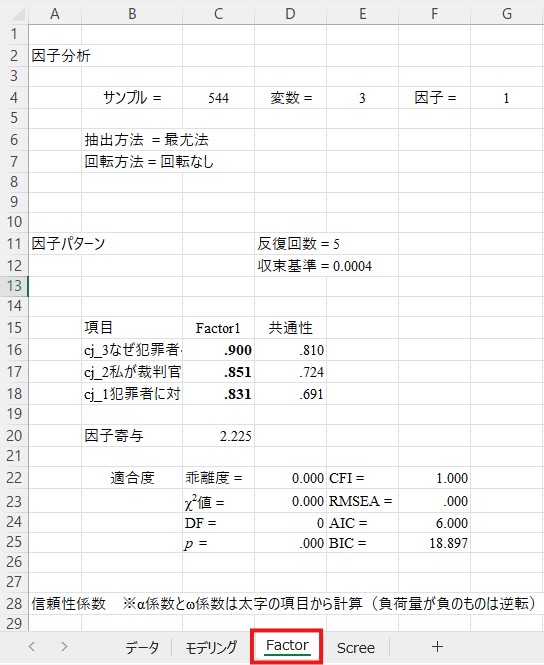
「Factor」というシートが新たに作成されれば成功です。
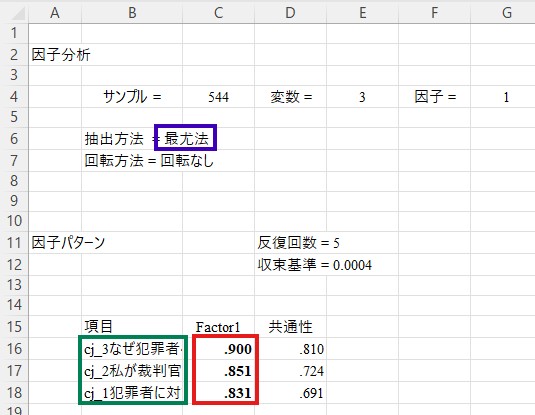
下の画像の赤で囲まれた部分が因子負荷量です。すべての因子負荷量が.400以上であるため、この因子構造で確定できます。
以上が1因子解の最もシンプルな因子分析ですが、因子が複数ある場合や因子負荷量が低い項目がある場合にはもう少し工夫をする必要があります。そのような場合にはこちらをご参照ください。
信頼性係数の算出
上記の通り、先行研究ですでに因子構造が分かっている場合には、信頼性係数を求めるだけで足ります。
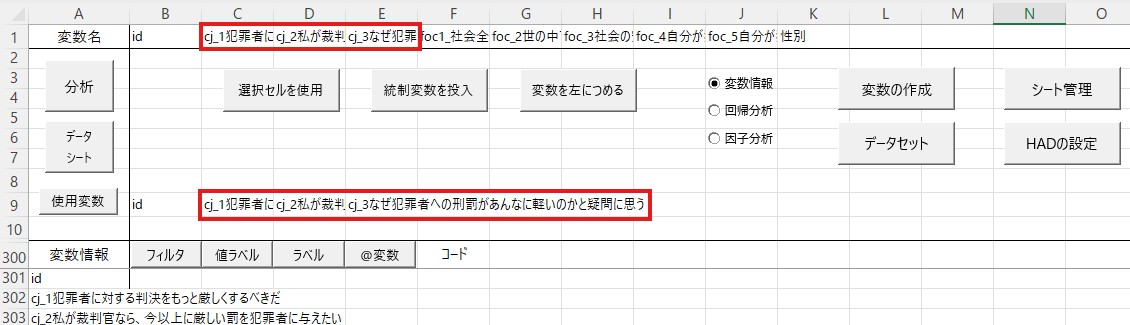
まず信頼性係数を求めたい項目を「使用変数」にコピペします。ここでは厳罰傾向を測定する3つの項目の信頼性係数を求めたいという想定で、3項目をコピペします。
左上の「分析」を左クリックしてください。
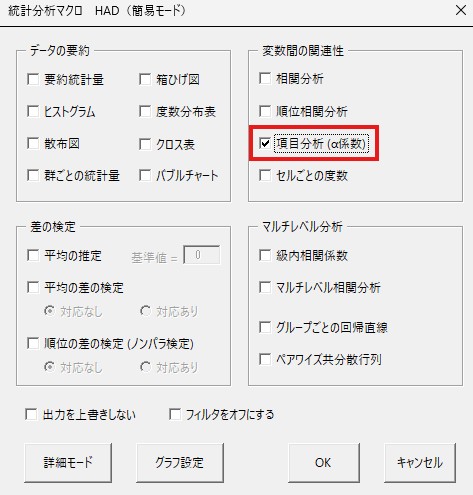
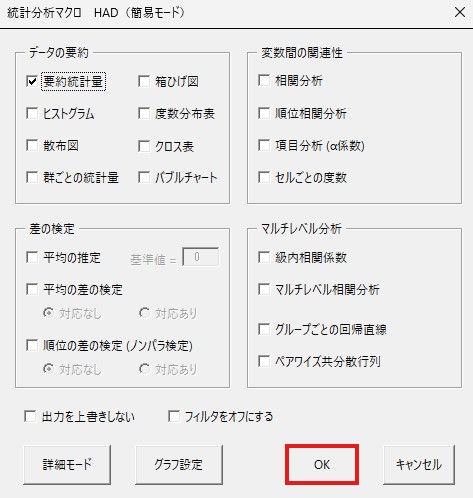
表示されたポップアップ画面で、右上の方にある「項目分析(α係数)」にチェックを入れます。
右下の「OK」を左クリックしてください。
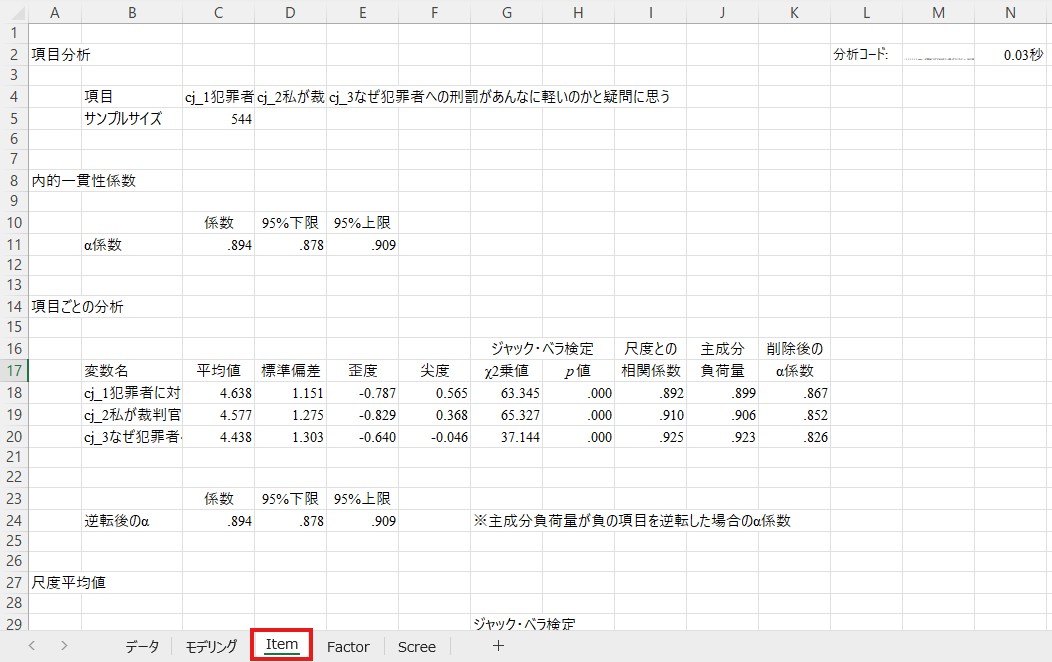
「Item」というシートが新たに作成されれば成功です。
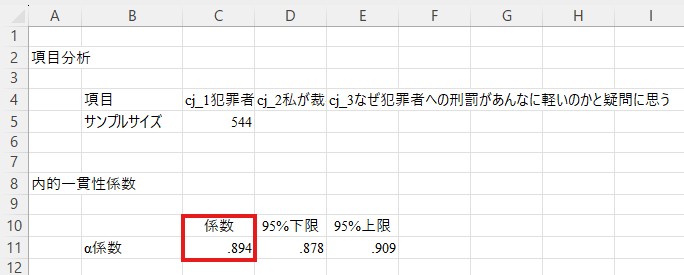
信頼性係数は上の方の「α係数」の横に表示されています。ここでは.864が厳罰傾向のα係数です。一般にα係数は.70以上であれば問題ないとされますので、ここでは特に問題はなさそうですので先に進みます。
なお、尺度に逆転項目がある場合には、少し下の「逆転後のα」の値を使う必要があります(ここでは逆転項目は入っていませんので、上の値と下の値は同じになっています)。
合成変数の作成
ここまでで厳罰傾向を測定する5つの項目を1つの変数として扱っていいことが分かりましたので、次はこれらの5項目の平均値を算出し、それを厳罰傾向の値とします。合成変数の作成にはエクセルのaverage関数を使うやり方もありますが(関数を使ったことがある方にとってはおそらくそちらの方が通常楽です)、ここではHADの機能を使ったやり方を解説します。
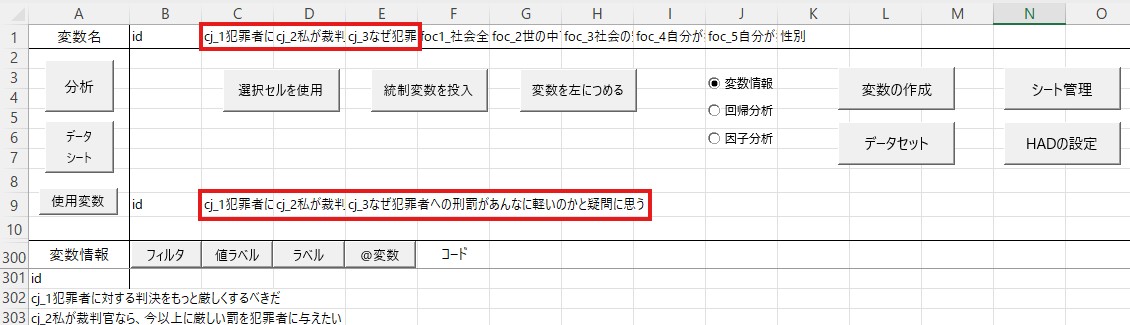
まず合成したい項目を「使用変数」にコピペします(上と同じです)。
「変数の作成」を左クリックしてください。
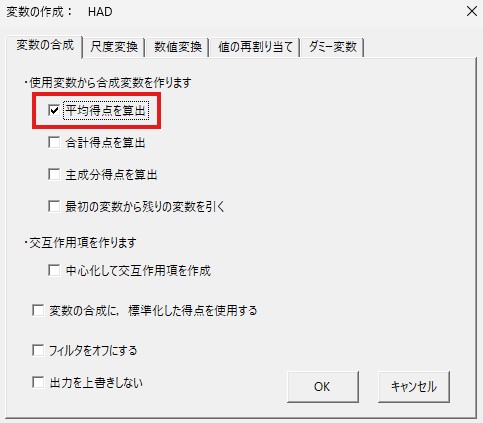
表示されたポップアップ画面で、「平均得点を算出」にチェックを入れてください。
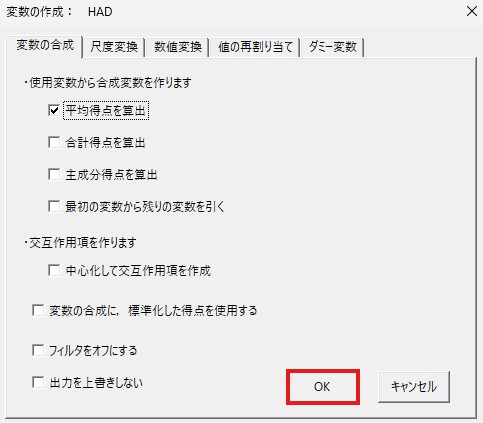
「OK」を左クリックします。
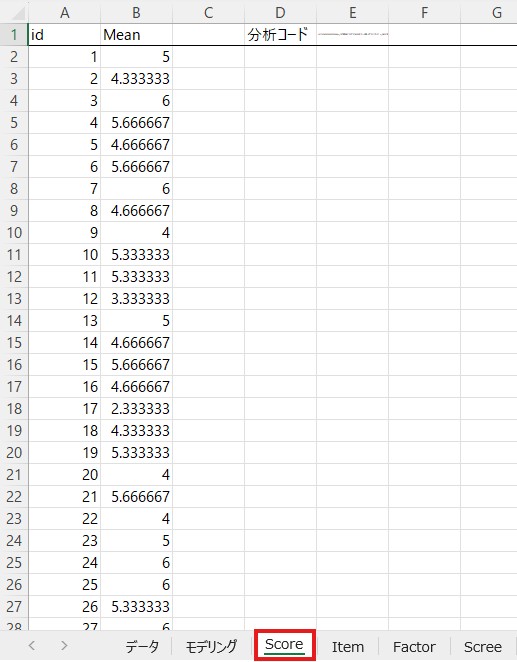
「Score」というシートが新たに作成されれば成功です。
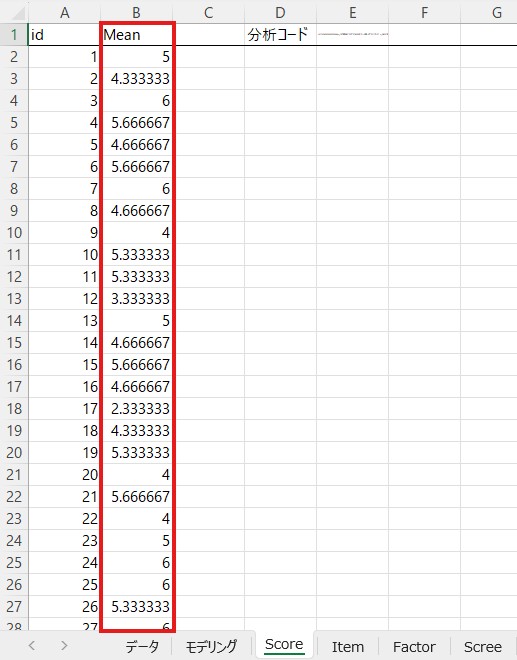
「Mean」の列には「使用変数」に入力した項目の平均値が入っています。ここでは5つの項目を入力しましたので、その5つの項目の平均値が計算されています。
「Mean」だと何の平均値が分からないので名前を「厳罰傾向」に変えておきます。
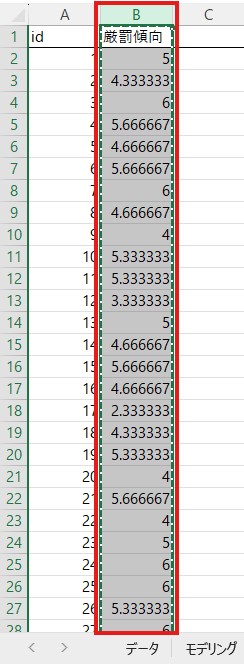
「厳罰傾向」の列全体を「データ」のシートに移す必要があるので、列全体をコピーします。
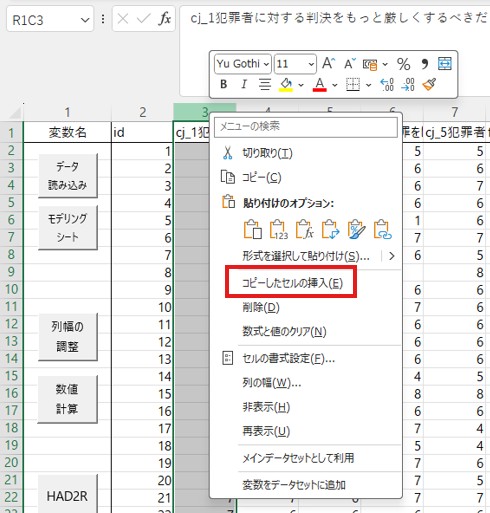
「データ」のシートに移動して、「ID」の右に貼り付けます。3列目で右クリックをし、「コピーしたセルの挿入」で「ID」の右に挿入できます。
下の画像のようになれば完成です。
以上の作業を変数(因子)の数だけ繰り返してください。例として用いているデータに含まれる犯罪不安は1因子構造ですので、もう1回処理を繰り返す必要があります。「foc_1」から「foc_5」が犯罪不安を測定する項目です。作業を完了すると以下の画像のようになります。
3.記述統計
ここまでで分析に使用する合成変数は作成されましたが、重回帰分析の前には他にもしないといけないことがあります。t検定と一緒によく行われる分析は、①記述統計(平均値、標準偏差)の算出です。①変数の平均値や標準偏差はデータに偏り・歪みがないかを把握するために必要な情報です。また、これらの情報はメタ分析の際にも必要になりますので、特段の事情がない限り論文には含めておくべきでしょう。
平均値と標準偏差
「データ」のシートで「データ読み込み」をクリックしたうえで、平均値と標準偏差を求めたい変数を「使用変数」の横に貼り付けます。
「分析」を左クリックしてください。
表示されたポップアップ画面で、左上の方にある「要約統計量」にチェックを入れてください。
右下にある「OK」を左クリックしてください。
「Summary」というシートが新たに作成されれば成功です。
「平均値」と「標準偏差」の列にそれぞれの値が表示されています。たとえばここでは厳罰傾向の平均値は4.551、標準偏差は1.131であることが分かります。
4.t検定の実行
ここまでの処理を行ってようやくt検定を行うことができます。
まず、t検定に使いたい変数を「使用変数」の横にコピペします。ここで重要なのは順番で、群分けのために使われる変数は一番右に置く必要があります。ここの分析では、厳罰傾向と犯罪不安が性別ごとに異なるのかを知りたいわけですので、「群分けのために使われる変数」は性別になります。これを一番右に置くようにしてください。
(なお、t検定は一度に1つの従属変数(ここでは厳罰傾向と犯罪不安です)しか扱えません。ですので、2つ以上の変数の差の検定をしたい場合には、t検定を繰り返す必要がありますが、HADは群分けのために使われる変数の左にある変数ごとに分析を繰り返してくれますので、基本的には複数回分析を繰り返す必要はありません。ただし、独立変数(ここでは性別です)を変えたい場合には、分析を繰り返す必要があります。)
次に「分析」を左クリックしてください。
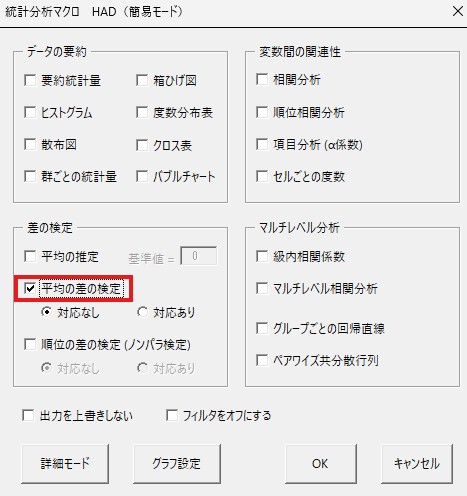
表示されたポップアップ画面で、左下の方にある「平均の差の検定」にチェックを入れてください。その下にある「対応なし」と「対応あり」については変えなくて大丈夫です。
「分析実行」を左クリックしてください。
従属変数の数だけ「Ttest」というシートが作成されます。ここでは厳罰傾向と犯罪不安という2つの従属変数がありますので、「Ttest1」(厳罰傾向の結果)、「Ttest2」(犯罪不安の結果)の2つのシートが新たに作成されれば成功です。
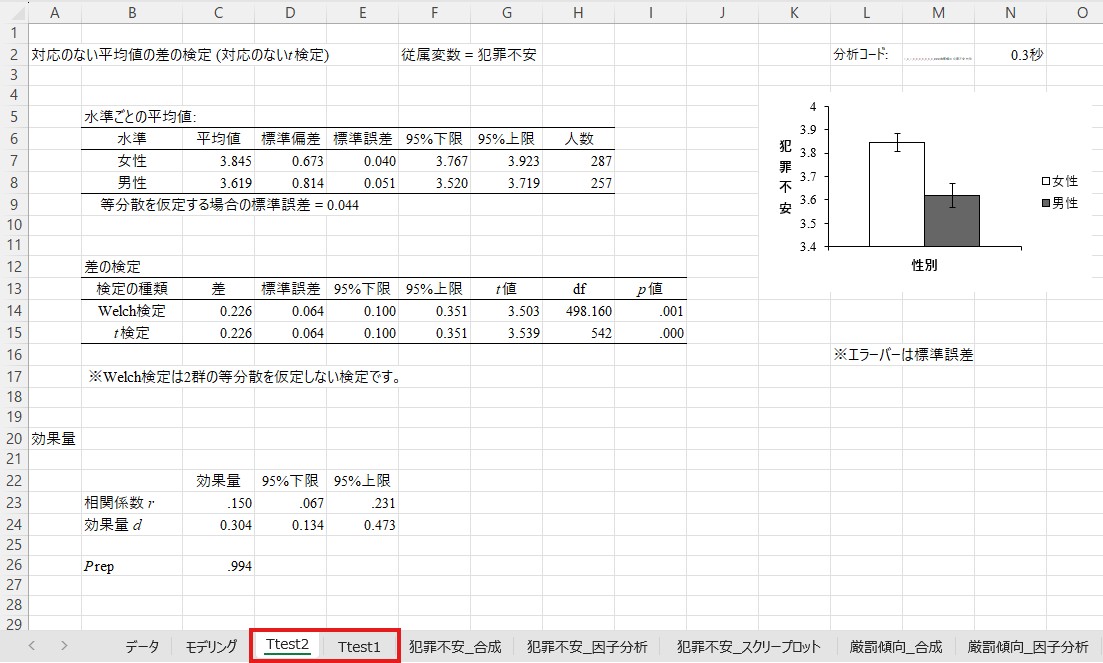
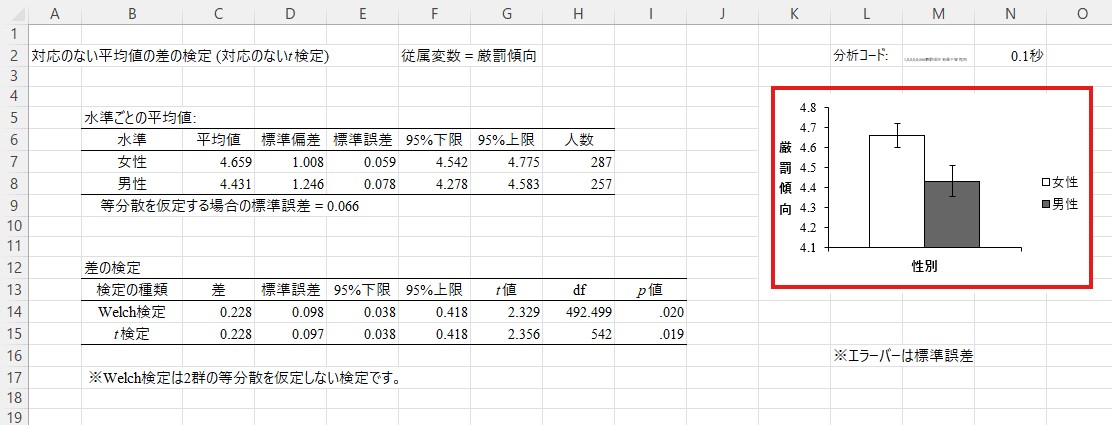
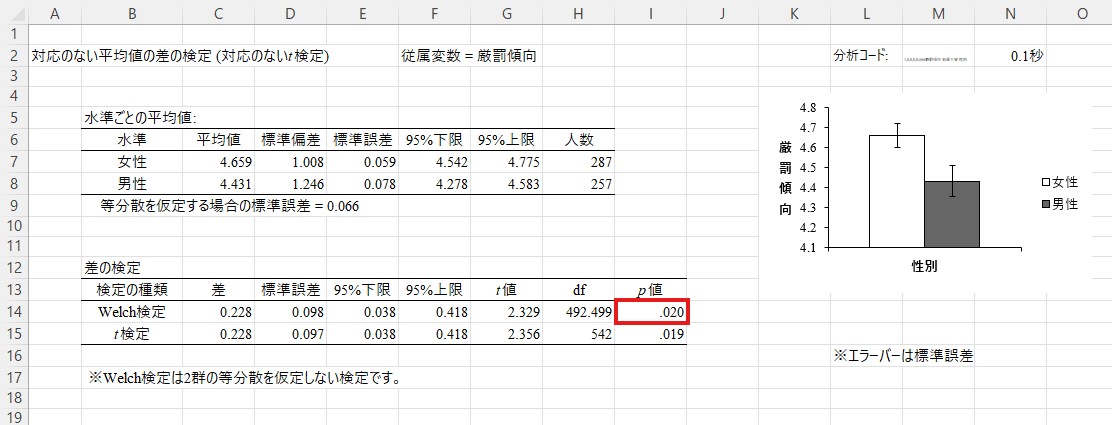
ここでは厳罰傾向に関する結果(「Ttest1)を見てみましょう。まず細かい数字を見る前に右にある図を見てください。ここでは条件ごとの平均値が図示されています。女性の方が男性よりも平均値が高くなっています。このデータでは値が大きいほどが厳罰的であることを示すようにコーディングされていますので、女性の方が厳罰的であるようです。
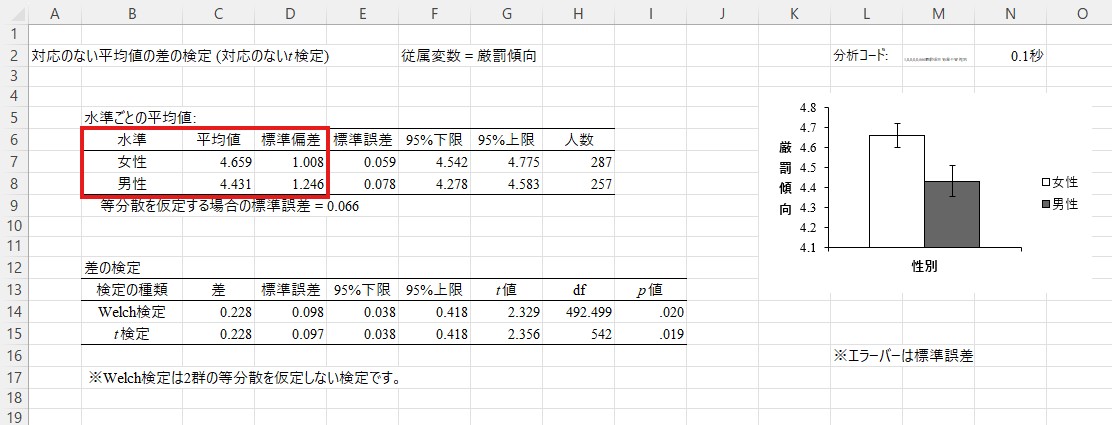
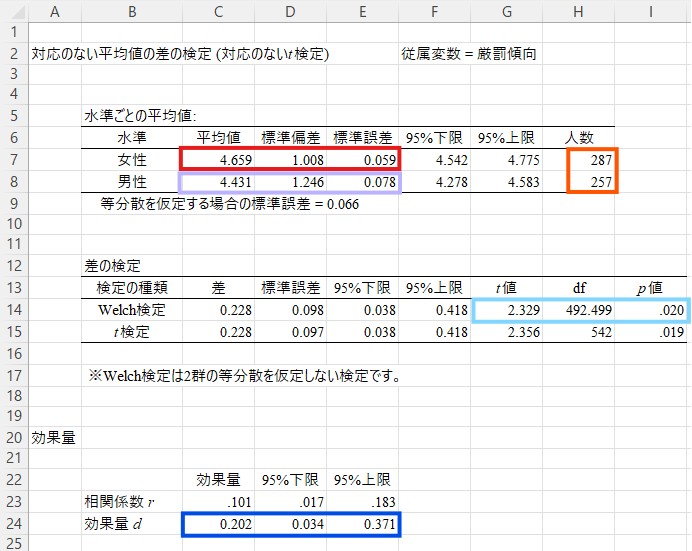
この図に対応する数値は少し左の「水準ごとの平均値」に書かれています。女性の平均値は4.659、男性の平均値は4.431です。標準偏差は女性が1.008、男性が1.246です。標準偏差は回答の散らばりの大きさを表し、値が大きいほど散らばりが大きいことを示す指標ですので、男性の回答者の方が若干回答の散らばりが大きい(つまり、個人差が大きい)ようです。
下の「差の検定」の箇所には、ここまでで分かった差が有意であるか(つまり、単なる偶然によって得られたものでないか)を確認するためのp値が書かれています。「Welch検定」と「t検定」という2つの行がありますが、上の「Welch検定」を見てください。その値は.020です。
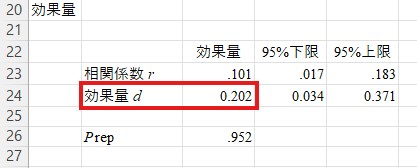
最後に、一番下の「効果量」を見てください。ここまでの分析では、厳罰傾向には有意な男女差があることが示されました。しかし、この差がどれくらい大きいのかは分かりません。これを補うのが効果量です。「効果量d」を見ると、0.202という値になっています。一般に効果量dは0.20程度であれば小さい、0.50程度であれば中程度、0.80程度であれば大きいと判断します。そのため、ここでの効果量は「小さい」ということになりそうです。
以上の結果をまとめると、厳罰傾向には有意な男女差はあるが、その差は小さいと判断することになります。
犯罪不安についても同じように解釈してください。
5.表の作成
ここまでで分析が終わりましたので、論文上で報告するための表を作成します。ここまでの分析をまとめたHADのファイルはこちらから、エクセルの表の見本はこちらからダウンロードできます。
ここまで行ってきたような分析の結果を報告する際には、記述統計の結果とt検定の結果を報告する必要がありますが、これらは1つの表にまとめられます。また、因子分析については、探索的因子分析を行った場合(つまり、先行研究で因子構造が示されていない場合)のみ報告する必要があります。ここでは必要だったという想定でまとめます。
表の効率的な作り方は人それぞれだと思いますので、見本を参考にしながらご自身で作成してください。以下ではHADの出力と表の対応のみを記載いたします。
因子分析
《表》
《HADの出力》
t検定
《表》
《HADの出力》
なお、今回のように複数の従属変数についてt検定を繰り返している場合には、以下のようにまとめて表にしてしまった方が見やすいと思います。
6.論文の記述
表が作成できたら最後に文章を記述します。以下はここまでの分析の結果の書き方の一例ですが、絶対的に正しい正解はありませんので、他の論文も参考にしながら自分なりの書き方を見つけてください。
変数の合成:因子分析の場合
厳罰傾向を測定する3項目について探索的因子分析を行った。まず固有値の減衰状況を確認したところ,2.48, 0.29, 0.23と,明確に1因子構造が示唆される結果であったため,1因子解を指定して分析を行った。その結果,Table 1に示される通り,すべての項目の因子負荷量は.40以上であった。そのため,全項目の平均値を算出し,以後の分析に使用した。
変数の合成:信頼性係数の場合
厳罰傾向を測定する5項目についてCronbachのα係数を算出したところ,その値はα = .89であり,十分な内的一貫性が確認された。そのため,全項目の平均値を算出し,以後の分析に使用した。
記述統計とt検定
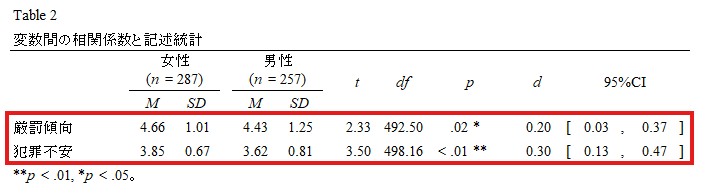
作成された2つの変数についてt検定を行った。まず厳罰傾向については,男性(M = 4.43, SD = 1.25)と比べて女性(M = 4.66, SD = 1.01)の方が平均値が高いことが示された(t(492.50) = 2.33, p = .02, d = 0.20, 95%CI [0.03, 0.37])。犯罪不安についても同様に,男性(M = 3.62, SD = 0.81)と比べて女性(M = 3.85, SD = 0.67)の方が平均値が高いことが示された(t(498.16) = 3.50, p < .01, d = 0.30, 95%CI [0.13, 0.47])
ページ上部に戻る